User Guide

Where to start?

It is important to understand that the key elements of this library are curve construction, financial instrument specification, foreign exchange (FX) and risk sensitivity. All of these functionalities are interlinked and potentially dependent upon each other. This guide’s intention is to introduce them in a structured way.

Let’s start with the fundamental constructors Curve and Instrument.

A trivial example

For example, we can construct Curves in many different ways: here we create one by directly specifying discount factors (DFs) on certain node dates (sometimes called pillar dates in other publications).

In [1]: from rateslib import *

In [2]: usd_curve = Curve(
   ...:     nodes={
   ...:         dt(2022, 1, 1): 1.0,
   ...:         dt(2022, 7, 1): 0.98,
   ...:         dt(2023, 1, 1): 0.95
   ...:     },
   ...:     calendar="nyc",
   ...:     id="sofr",
   ...: )
   ...: 

We can then construct an Instrument. Here we create a short dated RFR interest rate swap (IRS) using market specification pre-defined by rateslib.

In [3]: irs = IRS(
   ...:     effective=dt(2022, 2, 15),
   ...:     termination="6m",
   ...:     notional=1000000000,
   ...:     fixed_rate=2.0,
   ...:     spec="usd_irs"
   ...: )
   ...: 

You can read more about arguments for instruments here. To double check some of the arguments for a “usd_irs” one can run:

In [4]: defaults.spec["usd_irs"]
Out[4]: 
{'frequency': 'a',
 'stub': 'shortfront',
 'eom': False,
 'modifier': 'mf',
 'calendar': 'nyc',
 'payment_lag': 2,
 'currency': 'usd',
 'convention': 'act360',
 'leg2_frequency': 'a',
 'leg2_stub': 'shortfront',
 'leg2_eom': False,
 'leg2_modifier': 'mf',
 'leg2_calendar': 'nyc',
 'leg2_payment_lag': 2,
 'leg2_currency': 'usd',
 'leg2_convention': 'act360',
 'leg2_spread_compound_method': 'none_simple',
 'leg2_fixing_method': 'rfr_payment_delay'}

We can value the IRS with the Curve in its local currency (USD) by default, and see the generated cashflows.

In [5]: irs.npv(usd_curve)
Out[5]: 12629097.829705866

In [6]: irs.cashflows(usd_curve)
Out[6]: 
               Type Period  Ccy  Acc Start    Acc End    Payment Convention  DCF       Notional   DF Collateral  Rate  Spread     Cashflow         NPV  FX Rate     NPV Ccy
leg1 0  FixedPeriod   Stub  USD 2022-02-15 2022-08-15 2022-08-17     act360 0.50  1000000000.00 0.97       None  2.00     NaN -10055555.56 -9776494.15     1.00 -9776494.15
leg2 0  FloatPeriod   Stub  USD 2022-02-15 2022-08-15 2022-08-17     act360 0.50 -1000000000.00 0.97       None  4.58    0.00  23045139.84 22405591.98     1.00 22405591.98

If instead of this trivial, minimalist example you would like to see a real world example replicating a Bloomberg SWPM function SOFR curve please click the link.

Quick look at FX

Spot rates and conversion

The above values were all calculated and displayed in USD. That is the default currency in rateslib and the local currency of the swap. We can convert this value to another currency using the FXRates class. This is a basic class which is parametrised by some exchange rates.

In [7]: fxr = FXRates({"eurusd": 1.05, "gbpusd": 1.25})

In [8]: fxr.rates_table()
Out[8]: 
     eur  gbp  usd
eur 1.00 0.84 1.05
gbp 1.19 1.00 1.25
usd 0.95 0.80 1.00

We now have a mechanism by which to specify values in other currencies.

In [9]: irs.npv(usd_curve, fx=fxr, base="usd")
Out[9]: 12629097.829705866

In [10]: irs.npv(usd_curve, fx=fxr, base="eur")
Out[10]: <Dual: 12027712.218767, (fx_gbpusd, fx_eurusd), [0.0, -11454964.0]>

One observes that the value returned here is not a float but a Dual which is part of rateslib’s AD framework. One can read more about this particular treatment of FX here and more generally about the dual AD framework here. It is possible to call float() on this Dual to discard the sensitivity information and return just a regular float.

FX forwards

For multi-currency derivatives we need more than basic, spot exchange rates. We can also create an FXForwards class. This stores the FX rates and the interest rates curves that are used for all the FX-interest rate parity derivations. With these we can calculate forward FX rates and also ad-hoc FX swap rates.

In [11]: eur_curve = Curve({
   ....:     dt(2022, 1, 1): 1.0,
   ....:     dt(2022, 7, 1): 0.972,
   ....:     dt(2023, 1, 1): 0.98},
   ....:     calendar="tgt",
   ....: )
   ....: 

In [12]: eurusd_curve = Curve({
   ....:     dt(2022, 1, 1): 1.0,
   ....:     dt(2022, 7, 1): 0.973,
   ....:     dt(2023, 1, 1): 0.981}
   ....: )
   ....: 

In [13]: fxf = FXForwards(
   ....:     fx_rates=FXRates({"eurusd": 1.05}, settlement=dt(2022, 1, 1)),
   ....:     fx_curves={
   ....:         "usdusd": usd_curve,
   ....:         "eureur": eur_curve,
   ....:         "eurusd": eurusd_curve,
   ....:     }
   ....: )
   ....: 

In [14]: fxf.rate("eurusd", settlement=dt(2023, 1, 1))
Out[14]: <Dual: 1.084263, (fx_eurusd), [1.0]>

In [15]: fxf.swap("eurusd", settlements=[dt(2022, 2, 1), dt(2022, 5, 1)])
Out[15]: <Dual: -36.900308, (fx_eurusd), [-35.1]>

FXForwards objects are comprehensive and more information regarding all of the FX features is available in this link.

More about instruments

We saw an example of the IRS instrument above. A complete guide for all of the Instruments is available in this link. It is recommended to also, in advance, review Periods and then Legs, since the documentation for these building blocks provides technical descriptions of the parameters that are used to build up the instruments.

Multi-currency instruments

Let’s take a quick look at a multi-currency instrument: the FXSwap. All instruments have a mid-market pricing function rate(). Keeping a consistent function name across all Instruments allows any of them to be used within a Solver to calibrate Curves around target mid-market rates.

In [16]: fxs = FXSwap(
   ....:     effective=dt(2022, 2, 1),
   ....:     termination="3m",
   ....:     notional=20e6,
   ....:     currency="eur",
   ....:     leg2_currency="usd",
   ....: )
   ....: 

In [17]: fxs.rate(curves=[None, eurusd_curve, None, usd_curve], fx=fxf)
Out[17]: <Dual: -36.900308, (fx_eurusd), [-35.1]>

Securities and bonds

A very common instrument in financial investing is a FixedRateBond. At time of writing the on-the-run 10Y US treasury was the 3.875% Aug 2033 bond. Here we can construct this using the street convention and derive the price from yield-to-maturity and risk calculations.

In [18]: fxb = FixedRateBond(
   ....:     effective=dt(2023, 8, 15),
   ....:     termination=dt(2033, 8, 15),
   ....:     fixed_rate=3.875,
   ....:     spec="ust"
   ....: )
   ....: 

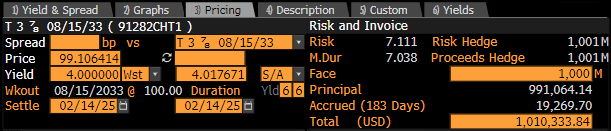
In [19]: fxb.accrued(settlement=dt(2025, 2, 14))
Out[19]: 1.9269701086956519

In [20]: fxb.price(ytm=4.0, settlement=dt(2025, 2, 14))
Out[20]: 99.10641380057267

In [21]: fxb.duration(ytm=4.0, settlement=dt(2025, 2, 14), metric="duration")
Out[21]: 7.178560455252011

In [22]: fxb.duration(ytm=4.0, settlement=dt(2025, 2, 14), metric="modified")
Out[22]: 7.037804367894129

In [23]: fxb.duration(ytm=4.0, settlement=dt(2025, 2, 14), metric="risk")
Out[23]: 7.11053190579773

There are some interesting Cookbook articles on BondFuture and cheapest-to-deliver (CTD) analysis.

Calibrating curves with a solver

The guide for Constructing Curves introduces the main curve classes, Curve, LineCurve, and IndexCurve. It also touches on some of the more advanced curves CompositeCurve, ProxyCurve, and MultiCsaCurve.

Calibrating curves is a very natural thing to do in fixed income. We typically use market prices of commonly traded instruments to set values.

Below we demonstrate how to calibrate the Curve that we created above in the initial trivial example using SOFR swap market data. First, we are reminded of the discount factors (DFs) currently set on that curve.

In [24]: usd_curve.nodes
Out[24]: 
{datetime.datetime(2022, 1, 1, 0, 0): 1.0,
 datetime.datetime(2022, 7, 1, 0, 0): 0.98,
 datetime.datetime(2023, 1, 1, 0, 0): 0.95}

Now we will instruct a Solver to recalibrate those value to match a set of instrument prices, s.

In [25]: usd_args = dict(
   ....:     effective=dt(2022, 1, 1),
   ....:     spec="usd_irs",
   ....:     curves="sofr"
   ....: )
   ....: 

In [26]: solver = Solver(
   ....:     curves=[usd_curve],
   ....:     instruments=[
   ....:         IRS(**usd_args, termination="6M"),
   ....:         IRS(**usd_args, termination="1Y"),
   ....:     ],
   ....:     s=[4.35, 4.85],
   ....:     instrument_labels=["6M", "1Y"],
   ....:     id="us_rates"
   ....: )
   ....: 
SUCCESS: `func_tol` reached after 3 iterations (levenberg_marquardt), `f_val`: 3.0486413284865872e-15, `time`: 0.0021s

Solving was a success! Observe that the DFs on the Curve have been updated:

In [27]: usd_curve.nodes
Out[27]: 
{datetime.datetime(2022, 1, 1, 0, 0): <Dual: 1.000000, (sofr0, sofr1, sofr2), [1.0, 0.0, 0.0]>,
 datetime.datetime(2022, 7, 1, 0, 0): <Dual: 0.978595, (sofr0, sofr1, sofr2), [0.0, 1.0, 0.0]>,
 datetime.datetime(2023, 1, 1, 0, 0): <Dual: 0.953176, (sofr0, sofr1, sofr2), [0.0, 0.0, 1.0]>}

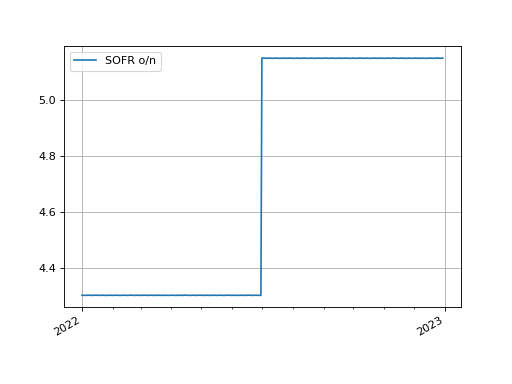
We can plot the overnight rates for the calibrated curve. This curve uses ‘log_linear’ interpolation so the overnight forward rates are constant between node dates.

In [28]: usd_curve.plot("1b", labels=["SOFR o/n"])
Out[28]: 
(<Figure size 640x480 with 1 Axes>,
 <Axes: >,
 [<matplotlib.lines.Line2D at 0x7f0aa004b610>])

(Source code, png, hires.png, pdf)

Pricing Mechanisms

Since rateslib is an object oriented library with object associations we give detailed instructions of the way in which the associations can be constructed in mechanisms.

The key takeway is that when you initialise and create an Instrument you can do one of three things:

1. Not provide any Curves for pricing upfront (curves=NoInput(0)).

2. Create an explicit association to pre-existing Python objects, e.g. curves=my_curve.

3. Define some reference to a Curves mapping with strings using curves="my_curve_id".

If you do 1) then you have to provide Curves at price time: instrument.npv(curves=my_curve).

If you do 2) then you do not need to provide anything further at price time: instrument.npv(), or can provide new Curves directly, like for 1).

If you do 3) then you can provide a Solver which contains the Curves and will resolve the string mapping: instrument.npv(solver=my_solver). Or you can also provide Curves directly, like for 1).

Best practice in rateslib is to use 3). This is the safest and most flexible approach and designed to work best with risk sensitivity calculations also.

Risk Sensitivities

Rateslib’s main objective is to capture delta and gamma risks in a generalised and holistic mathematical framework. See the risk framework notes.

Utilities

Rateslib could not function without some utility libraries. These are often referenced in other guides as they arise and can also be linked to from those sections.

Specifically those utilities are:

• Holiday calendars and day count conventions

• Schedule building

• Piecewise polynomial splines for curve interpolation

• Forward mode automatic differentiation (AD) and Dual numbers

• Defaults used for instrument specification

Cookbook

This is a collection of more detailed examples and explanations that don’t necessarily fall into any one category. See the Cookbook index.